Grids#
Datashader renders data into regularly sampled arrays, a process known as rasterization, and then optionally converts that array into a viewable image (with one pixel per element in that array).
In some cases, your data is already rasterized, such as data from imaging experiments, simulations on a regular grid, or other regularly sampled processes. Even so, the rasters you have already are not always the ones you need for a given purpose, having the wrong shape, range, or size to be suitable for overlaying with or comparing against other data, maps, and so on. Datashader provides fast methods for “regridding”/”re-sampling”/”re-rasterizing” your regularly gridded datasets, generating new rasters on demand that can be used together with those it generates for any other data types. Rasterizing into a common grid can help you implement complex cross-datatype analyses or visualizations.
In other cases, your data is stored in a 2D array similar to a raster, but represents values that are not regularly sampled in the underlying coordinate space. Datashader also provides fast methods for rasterizing these more general rectilinear or curvilinear grids, known as quadmeshes as described later below. Fully arbitrary unstructured grids (Trimeshes) are discussed separately.
Re-rasterization#
First, let’s explore the regularly gridded case, declaring a small raster using Numpy and wrapping it up as an xarray DataArray for us to re-rasterize:
import numpy as np, datashader as ds, xarray as xr
from datashader import transfer_functions as tf, reductions as rd
def f(x,y):
return np.cos((x**2+y**2)**2)
def sample(fn, n=50, range_=(0.0,2.4)):
xs = ys = np.linspace(range_[0], range_[1], n)
x,y = np.meshgrid(xs, ys)
z = fn(x,y)
return xr.DataArray(z, coords=[('y',ys), ('x',xs)])
da = sample(f)
Here we are declaring that the first dimension of the DataArray (the rows) is called y and corresponds to the indicated continuous coordinate values in the list ys, and similarly for the second dimension (the columns) called x. The coords argument is optional, but without it the default integer indexing from Numpy would be used, which would not match how this data was generated (sampling over each of the ys).
DataArrays like da happen to be the format used for datashader’s own rasterized output, so you can now immediately turn this hand-constructed array into an image using tf.shade() just as you would for points or lines rasterized by datashader:
tf.shade(da)
Interpolation (upsampling)#
So, what if we want a larger version? We can do that with the Datashader Canvas.raster method. Note that Canvas.raster only supports regularly spaced rectilinear, 2D or 3D DataArrays, and so will not accept the additional dimensions or non-separable coordinate arrays that xarray allows (for which see Quadmesh, below). Also see the Quadmesh docs below if you want to use a GPU for processing your raster data, because the Datashader Canvas.raster implementation does not yet support GPU arrays.
Assuming you are ready to use Canvas.raster, let’s try upsampling with either nearest-neighbor or bilinear interpolation (the default):
tf.Images(tf.shade(ds.Canvas().raster(da, interpolate='linear'), name="linear interpolation (default)"),
tf.shade(ds.Canvas().raster(da, interpolate='nearest'), name="nearest-neighbor interpolation"))
OMP: Info #276: omp_set_nested routine deprecated, please use omp_set_max_active_levels instead.
| linear interpolation (default) | nearest-neighbor interpolation |
As you can see, linear interpolation works well for smoothly varying values, like those in the lower left of this function, but doesn’t help much for regions close to or beyond the sampling limits of the original raster, like those in the upper right.
We can choose whatever output size we like and sample the grid over any range we like, though of course there won’t be any data in regions outside of the original raster grid:
tf.shade(ds.Canvas(plot_height=200, plot_width=600, x_range=(-2,5), y_range=(-0.1,0.4)).raster(da))
Aggregation (downsampling)#
The previous examples all use upsampling, from a smaller to a larger number of cells per unit distance in X or Y. Downsampling works just as for points and lines in Datashader, supporting various aggregation functions. These aggregation functions determine the result when more than one raster grid cell falls into a given pixel’s region of the plane. To illustrate downsampling, let’s first render a 500x500 version of the above 50x50 array:
da2 = sample(f, n=500)
tf.shade(da2)
You can see that the version we upsampled to this size from the 50x50 samples is similar to this, but this one is much smoother and more accurately represents the underlying mathematical function, because it has sufficient resolution to avoid aliasing in the high-frequency portions of this function (towards the upper right).
Now that we have this larger array, we can downsample it using a variety of aggregation functions:
cvs = ds.Canvas(plot_width=150, plot_height=150)
tf.Images(tf.shade(cvs.raster(da2), name="mean downsampling (default)"),
tf.shade(cvs.raster(da2, agg=rd.min()), name="min downsampling"),
tf.shade(cvs.raster(da2, agg=rd.max()), name="max downsampling"),
tf.shade(cvs.raster(da2, agg=rd.mode()), name="mode downsampling"),
tf.shade(cvs.raster(da2, agg=rd.std()), name="std downsampling"))
| mean downsampling (default) | min downsampling | max downsampling | mode downsampling | std downsampling |
Here the default downsampling function mean renders a faithful size-reduced version of the original, with all the raster grid points that overlap a given pixel being averaged to create the final pixel value. The min and max aggregation functions take the minimum or maximum, respectively, of the values overlapping each pixel, and you can see here that the min version has larger light-blue regions towards the upper right (with each pixel reflecting the minimum of all grid cells it overlaps), while the max version has larger dark-blue regions towards the upper right. The mode version computes the most common value that overlaps this pixel (not very useful for floating-point data as here, but important for categorical data where mean would not be valid; in that case you can also use first or last to take the first or last value found for a given pixel). The std version reports the standard deviation of the grid cells in each pixel, which is low towards the lower left where the function is smooth, and increases towards the upper right, where the function value varies significantly per pixel (i.e., has many samples in the original grid with different values).
The differences between min and max are clearer if we look at a regime where the function varies so much that it can only barely be faithfully be represented in a grid of this size:
da3 = sample(f, n=500, range_=(0,3))
tf.shade(da3)
In the upper right of this plot, you can see that the function is varying with such high frequency that any downsampled version will fail to represent it properly. The aggregation functions in Datashader can help you see when that is happening:
cvs = ds.Canvas(plot_width=150, plot_height=150)
tf.Images(tf.shade(cvs.raster(da3), name="mean downsampling (default)"),
tf.shade(cvs.raster(da3, agg=rd.min()), name="min downsampling"),
tf.shade(cvs.raster(da3, agg=rd.max()), name="max downsampling"),
tf.shade(cvs.raster(da3, agg=rd.mode()),name="mode downsampling"),
tf.shade(cvs.raster(da3, agg=rd.std()), name="std downsampling"))
| mean downsampling (default) | min downsampling | max downsampling | mode downsampling | std downsampling |
Here you can see that the mean downsampling looks like a good approximation to the original array, locally averaging the original function values in each portion of the array. However, if you were to zoom in and adjust for contrast, you would be able to see some of the inevitable aliasing artifacts that occur for any such representation in a too-small array. These aliasing effects are clearly visible in the min and max aggregation, because they keep the local minimum or maximum rather than averaging out the artifacts. Comparing mean and min or max (or subtracting min from max) can help find regions of the array that are being poorly represented in the current view.
Collections of raster data#
The above examples all use a single 2D DataArray. Datashader’s raster support can also use a 3D DataArray as long as which “layer” along this third dimension is wanted is specified:
def g(x, y, k=1):
return np.cos(k*((x**2+y**2)**2))
ks = [1.1,3.3,33]
xs = ys = np.linspace(0.0, 2.4, 200)
y,k,x = np.meshgrid(ys, ks, xs, indexing='xy')
da4 = xr.DataArray(g(x,y,k), coords=[('k',ks), ('y',ys), ('x',xs)])
tf.Images(tf.shade(ds.Canvas().raster(da4, layer=1.1), name="k=1.1"),
tf.shade(ds.Canvas().raster(da4, layer=3.3), name="k=3.3"),
tf.shade(ds.Canvas().raster(da4, layer=33), name="k=33"))
| k=1.1 | k=3.3 | k=33 |
Here the factor “k” results in the function being evaluated at increasingly higher frequencies, eventually leading to complex Moiré patterns due to undersampling for k=33. 3D xarrays are useful for reading multi-layer image files, such as those from xarray’s rasterio-based support for reading from multilayer TIFFs.
Similarly, Datashader can accept an xarray Dataset (a dictionary-like collection of aligned DataArrays), as long as the aggregation method specifies a suitable DataArray within the Dataset:
def h(x,y): return np.sin((x**2+y**2)**2)
def m(x,y): return np.exp(x+y)
dd = xr.Dataset({'cos': sample(f, n=150),
'sin': sample(h, n=150),
'exp': sample(m, n=150)})
tf.Images(tf.shade(ds.Canvas().raster(dd, agg=rd.mean('cos')), name='cos ((x^2+y^2)^2)'),
tf.shade(ds.Canvas().raster(dd, agg=rd.mean('sin')), name='sin ((x^2+y^2)^2)'),
tf.shade(ds.Canvas().raster(dd, agg=rd.mean('exp')), name='exp (x+y)'))
| cos ((x^2+y^2)^2) | sin ((x^2+y^2)^2) | exp (x+y) |
Scaling up#
The above rasters are all relatively tiny, for illustration purposes, but Datashader’s raster support is accelerated using multi-core machine-code generation from Numba, and can re-sample much larger rasters easily. For instance, rendering the above function into a 10000x10000 raster takes a few seconds on a four-core machine using Numpy, but it can then be re-sampled using Datashader in under 0.1 sec:
%time da5 = sample(m, n=10000, range_=(0,3))
%time tf.shade(cvs.raster(da5))
CPU times: user 614 ms, sys: 3.68 s, total: 4.29 s
Wall time: 17.3 s
CPU times: user 218 ms, sys: 448 ms, total: 666 ms
Wall time: 306 ms
Interactivity#
In practice, it is usually a good idea to view your data interactively at many different zoom levels to see all the data available and to detect any sampling or aliasing issues, which you can do with Datashader as described in 3_Interactivity. For such cases, you can define both upsampling and downsampling methods at the same time; whichever one is needed for a given zoom level and range of the data will be applied.
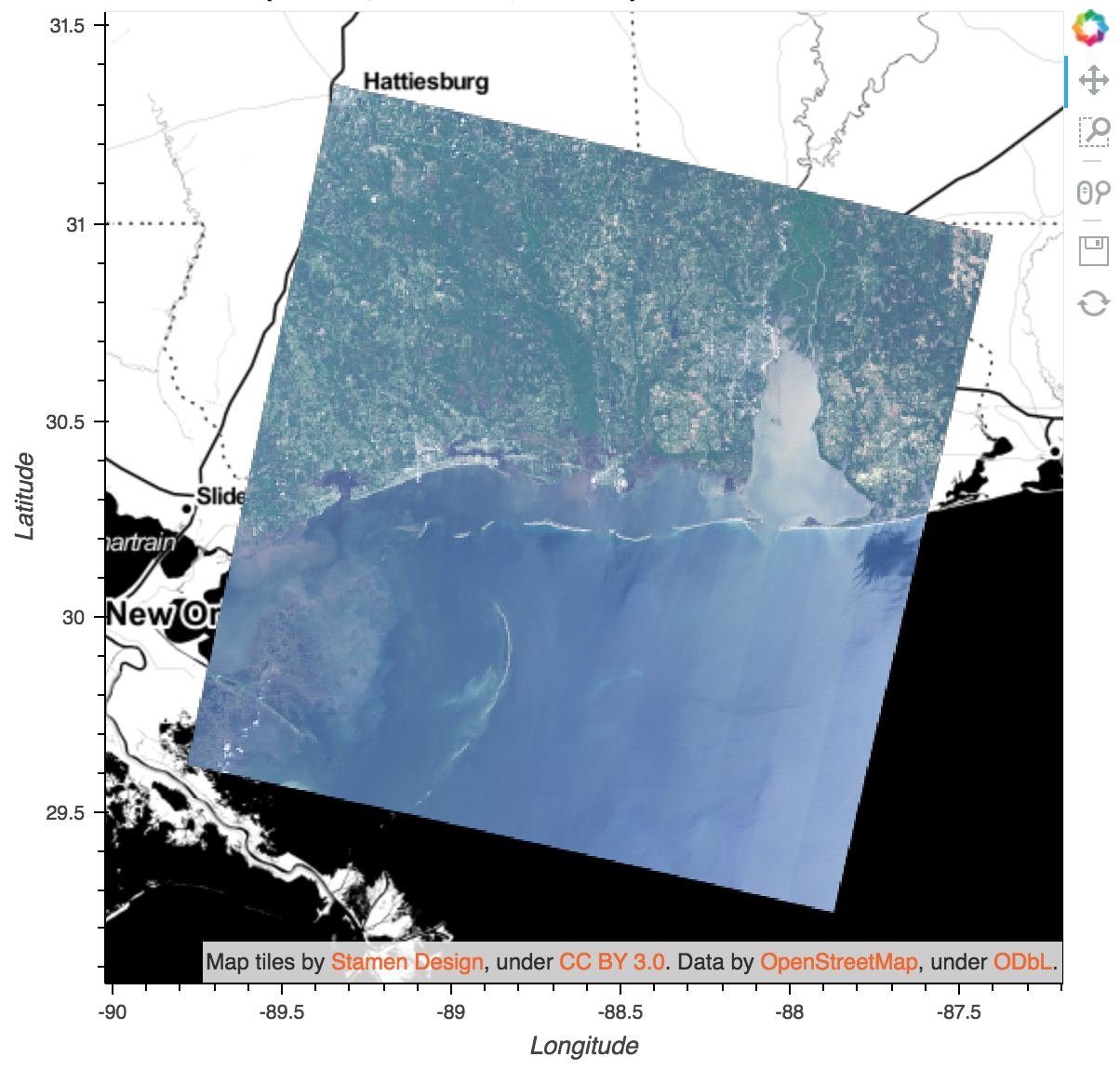
You can see Datashader rasters at work in the Landsat example notebook, which also has examples of reading raster data from TIFF files using xarray and rasterio:
Quadmesh Rasterization#
The Canvas.raster method described above supports re-rasterizing grids that are already regularly spaced. For the more general case of rectilinear and curvilinear grids, which are structured (unlike Trimesh grids) but not necessarily regularly spaced, Datashader provides the Canvas.quadmesh method. Despite its similarities with raster, quadmesh is currently implemented separately from raster, and thus has quite different features and limitations. For instance, quadmesh supports GPU arrays (including an optimized code path specifically speeding up regularly spaced rasters if they are provided), while raster offers optional interpolation and supports distributed computing using Dask, and many other small differences exist (see the docs for each method). So if you have a regularly spaced array, you will probably want to try both quadmesh and raster and see which one meets your needs.
Rectilinear Quadmesh#
A rectilinear quadmesh is specified as a 2-dimensional xarray DataArray with two 1-dimensional coordinates. The coordinates specify the center position of the quads in each row or column of the grid, allowing the spacing on x and y to be irregular, but leaving the two dimensions orthogonal (and thus always producing an axis-aligned rectangular image out of the provided rectangular array, with each patch also rectangular and axis aligned).
da = xr.DataArray(
[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],
coords=[('y', [1, 6, 7]),
('x', [1, 2, 7])],
name='Z')
canvas = ds.Canvas()
tf.shade(canvas.quadmesh(da, x='x', y='y'))
Because the quads may vary in size, a given quadmesh rasterization call may require a combination of upscaling and downscaling at different locations in the grid. Canvas.raster, in contrast, is always either upscaling or downscaling in a given call, never both. Quadmesh upscaling is performed with nearest-neighbor interpolation, and downscaling is performed using the aggregation function supplied as the agg argument to Canvas.quadmesh. If not supplied, the aggregation function defaults to mean.
def rect_data(n):
xs = np.linspace(0, 3, n) ** 2
ys = np.arange(n)
zs = np.sin(xs * ys[:, np.newaxis])
da = xr.DataArray(zs, coords=[('y', ys), ('x', xs)], name='Z')
return da
canvas = ds.Canvas(plot_width=150, plot_height=150)
tf.Images(*[tf.shade(canvas.quadmesh(rect_data(n),x='x', y='y', agg=ds.mean('Z')), name=str(n))
for n in [20, 80, 320, 1280]])
| 20 | 80 | 320 | 1280 |
Curvilinear Quadmesh#
A curvilinear quadmesh is specified as an 2-dimensional xarray DataArray with 2-dimensional coordinates. When upsampling such a mesh, each array element will map to a quadrilateral patch (a “quad”), which need not be rectangular or axis aligned. The coordinates specify the center position of each quad in the grid, allowing the quadmesh to map from the underlying 2D array into any arbitrary overall shape and with arbitrarily varying grid spacing.
Qy = [[1, 2, 4],
[1, 2, 3],
[1, 2, 3]]
Qx = [[1, 1, 1],
[2, 2, 2],
[2.5, 3, 3]]
Z = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
da = xr.DataArray(Z, name='Z', dims = ['y', 'x'],
coords={'Qy': (['y', 'x'], Qy),
'Qx': (['y', 'x'], Qx)})
canvas = ds.Canvas()
tf.shade(canvas.quadmesh(da, x='Qx', y='Qy'))
As with the rectilinear quadmesh, upscaling is performed with nearest-neighbor interpolation, and downscaling is performed using the aggregation function supplied as the agg argument to Canvas.quadmesh (thus combining the values from multiple quads into a given pixel). If not supplied, the aggregation function defaults to mean.
def curve_data(n):
coords = np.linspace(-1.5,1.5,n)
X,Y = np.meshgrid(coords, coords);
Qx = np.cos(Y) - np.cos(X)
Qy = np.sin(Y) + np.sin(X)
Z = np.sqrt(X**2 + Y**2)
return xr.DataArray(Z, name='Z', dims=['Y', 'X'],
coords={'Qx': (['Y', 'X'], Qx),
'Qy': (['Y', 'X'], Qy)})
tf.Images(*[tf.shade(canvas.quadmesh(curve_data(n), x='Qx', y='Qy', agg=ds.mean('Z')), name=str(n))
for n in [8, 16, 32, 64]])
| 8 | 16 | 32 | 64 |